Билет 3 Вопрос 2
Полупроводники.
Общие представления
К полупроводникам относят вещества, в которых в равновесии при температуре Т=0 заполненные электронные состояния отделены от незаполненных запрещенной зоной с шириной, меньшей 3 эВ. При большей ширине запрещенной зоны вещество относят к диэлектрикам, хотя иногда и называют широкозонным полупроводником. Последняя заполненная электронная зона называется валентной, а первая незаполненная зона - зоной проводимости. Ширина запрещенной зоны Eg - это разница энергий электронных состояний, отвечающих минимуму энергии в зоне проводимости и максимуму энергии в валентной зоне, соответственно.
Если эти состояния отвечают одному и тому же значению волнового вектора (рис.20 а) то щель (запрещенная область энергий) называется прямой (d), а если разным значениям (рис.20 б), то непрямой (i).
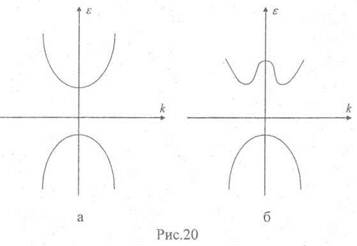
Ниже приведена таблица, характеризующая тип щели для наиболее часто встречающихся полупроводников:
|
Полупроводник |
Еg(3B) |
Тип щели |
|
|
при Т=0 К |
при Т=300 К |
||
|
Si |
1,17 |
1,14 |
i |
|
Ge |
0,74 |
0,67 |
i |
|
InSb |
0,23 |
0,18 |
d |
|
GaAs |
1,52 |
1,43 |
d |
|
PbTe |
0,19 |
0,30 |
d |
|
Алмаз |
5,4 |
i |
|
Концентрация собственных носителей заряда
При Т=0 в равновесии носители заряда (далее НЗ) в идеальном полупроводнике отсутствуют, и его электропроводность равна нулю. При Т≠0 некоторое количество электронов возбуждается тепловым образом из валентной зоны в зону проводимости. При переходе одного электрона возникает пара квазичастиц: электрон в зоне проводимости и дырка в валентной зоне, которые являются НЗ и называются собственными НЗ.
Электронные возбуждения сосредоточены в полосе энергий шириной порядка Т вблизи дна зоны проводимости, а дырочные возбуждения в такой же полосе вблизи потолка валентной зоны.
Плотность электронных состояний вблизи дна зоны проводимости имеет следующий вид для ε >Еg:
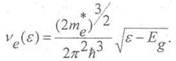
Найдем концентрацию электронных возбуждений при температуре Т по формуле:
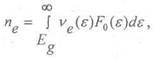
где F0(ε) - функция распределения Ферми-Дирака.
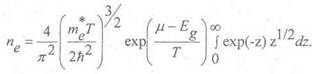
Получившийся
интеграл представляет собой гамма-функцию от аргумента 3/2 и равен ![]() . Следовательно:
. Следовательно:
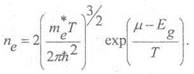
Концентрация дырок:
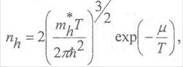
Перемножая ne и nh, получим выражение, справедливое в равновесном состоянии и для легированного полупроводника:

![]()
При комнатной температуре:
в германии и в кремнии, соответственно.
Для собственных НЗ справедливо условие электронейтральности ne=nh
Нельзя создать отдельно электрон или дырку. При тепловом возбуждении рождается электрон-дырочная пара.
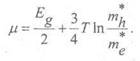
Значение химпотенциала:
Таким образом, при Т=0 уровень Ферми в собственном полупроводнике (в полупроводнике с преобладанием собственных НЗ) расположен посередине запрещенной зоны. С ростом температуры он сдвигается к той зоне, в которой эффективная масса носителей меньше.
Пусть теперь в полупроводник введен донор, то есть примесь замещения, обладающая большой валентностью: например в четырехвалентный германий или кремний - пятивалентная примесь мышьяка. Четыре электрона из пяти, присутствующих на внешней незаполненной оболочке атома примеси, образуют ковалентные связи с ближайшими атомами матрицы. Оставшийся пятый электрон в основном состоянии локализован на примеси и не является носителем заряда. Однако оторвать его от примеси и сделать делокализованным, то есть описывающимся блоховской волновой функцией, значительно проще, чем разрушить ковалентную связь и высвободить электрон из нее.
На языке энергетической диаграммы (рис. 21 а) это означает, что энергетический уровень электрона на примеси лежит в запрещенной зоне, и разность энергий между дном зоны проводимости и этим уровнем с энергией ε d меньше (а иногда и существенно меньше), чем ширина запрещенной зоны. При возбуждении электрона с примесного уровня в зону проводимости возникает НЗ - электрон, а донор из нейтрального становится положительно заряженным. Такой НЗ называется примесным.
Если же мы введем в кристалл акцептор, то есть примесь замещения с меньшей валентностью, например, трехвалентный индий в кристалл германия или кремния, то возникнут только три ковалентные связи с ближайшими атомами матрицы. Для образования четвертой ковалентной связи не хватает электрона. Поэтому примесь готова принять электрон, отобрав его у атома матрицы.
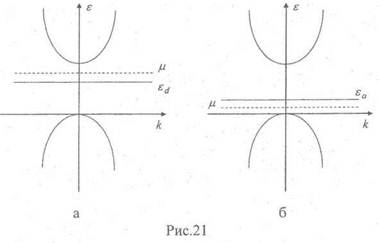
На энергетической диаграмме (рис. 21 б) это можно изобразить следующим образом: незаполненный уровень акцептора с энергией εа расположен внутри запрещенной зоны, и возбудить электрон из валентной зоны на этот уровень значительно проще, чем в зону проводимости. При таком процессе в валентной зоне возникает НЗ - дырка, а акцептор становится отрицательно заряженным.
Таким образом, в полупроводнике, который содержит доноры или акцепторы, имеются и собственные, и примесные НЗ. Поскольку для создания примесного НЗ требуется меньшая энергия, в области низких температур преобладают примесные носители (примесный полупроводник).
С ростом температуры могут начать преобладать собственные НЗ. Полупроводник из примесного может стать собственным. Характерная температура перехода зависит от концентрации доноров (акцепторов), положения примесного уровня и ширины запрещенной зоны. Она может оказаться больше комнатной (и даже температуры плавления полупроводника). Нас интересует, какой тип носителей преобладает в рабочем диапазоне температур. Если преобладает примесные НЗ электронного типа, то полупроводник называют полупроводником п – типа, а если примесные носители дырочного типа - то полупроводником р – типа.
Условие электронейтральности в присутствии доноров и (или) акцепторов имеет следующий вид:
![]()
Где Ndион и Nаион концентрации ионизованных (заряженных) доноров и акцепторов, соответственно.
При Т=0 уровень Ферми расположен посередине между донорным уровнем и дном зоны проводимости (рис. 21 а), а с ростом температуры он сдвигается вниз к середине запрещенной зоны. Подставляя значение μ, находим концентрацию примесных носителей в полупроводнике n – типа
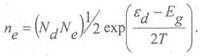
Таким образом, при Т=0 уровень Ферми расположен посередине между акцепторным уровнем и потолком валентной зоны (рис. 21 б), а с ростом температуры он сдвигается вверх к середине запрещенной зоны.
Концентрация примесных НЗ в полупроводнике p-типа равна
![]()
Рассмотрим качественно еще несколько вариантов. Что будет, если донорный уровень расположен выше дна зоны проводимости? В этом случае уже при Т=0 доноры ионизуются, а электроны переходят в зону проводимости, образуя частично заполненную зону с соответствующей поверхностью Ферми. Такой полупроводник называется вырожденным полупроводником n-типа. Аналогичная ситуация возникает в полупроводнике р-типа, когда акцепторный уровень расположен ниже потолка валентной зоны. Тогда часть электронов, обладающих при Т= 0 наибольшей энергией, переходит на акцепторный уровень, валентная зона оказывается частично заполненной, и в ней возникает дырочная поверхность Ферми.
Если же ввести в полупроводник и доноры, и акцепторы, причем εd > εa электронам с доноров выгодно перейти на акцепторы. При этом они понижают свою энергию. Если Nd > Na, то окажутся ионизованными все акцепторы и часть доноров (Ndион= Ndион= Nа). В противном случае (Nd < Na) ионизованы все доноры и часть акцепторов: Ndион= Ndион= Nа. В результате в полупроводнике возникает большое число заряженных примесей - ионизованных доноров и акцепторов. Такой процесс называется компенсацией, а полупроводник - компенсированным. В области компенсации концентрация носителей ниже, чем n и p пространственных областях.
Подвижность носителей
Электропроводность вещества пропорциональна числу НЗ, поэтому наблюдаемая в эксперименте температурная зависимость электропроводности полупроводника обусловлена, в основном, экспоненциальной зависимостью числа НЗ.
Для
описания процесса перемещения отдельного НЗ в электрическом поле вводят
характеристику, называемую подвижностью. Она определяется как коэффициент
пропорциональности между величиной скорости направленного движения НЗ |<![]() >|
и
>|
и
величиной
напряженности электрического поля ![]() (в
изотропном случае направление скорости параллельно или антипаралельно направлению
поля в зависимости от знака носителя):
(в
изотропном случае направление скорости параллельно или антипаралельно направлению
поля в зависимости от знака носителя):
![]()
Используя соотношение ![]() =
nq<
=
nq<![]() >, где
>, где ![]() - плотность
электрического тока, п -
концентрация носителей, a q- заряд носителя, получаем соотношение между электропроводностью и
подвижностью:
- плотность
электрического тока, п -
концентрация носителей, a q- заряд носителя, получаем соотношение между электропроводностью и
подвижностью:
![]()
В случае наличия нескольких сортов НЗ их вклады в электропроводность складываются.
По порядку величины подвижность НЗ можно оценить как
![]()
где т - эффективная масса носителя а τ - время его свободного пробега (время релаксации по импульсу).
Так как в полупроводнике число НЗ невелико то столкновения между ними маловероятны (в отличие от металлов). Поэтому основную роль в процессах релаксации НЗ играет их взаимодействие с примесями (область низких температур) или с фононами (область высоких температур). Оба этих вклада в сопротивление аддитивны как и в случае металлов.
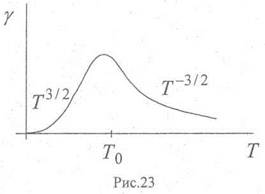
При Т >>θD, когда рассеяние на фононах играет определяющую роль, подвижность НЗ
![]()
При низкой температуре (T<<θD) основную роль в процессах рассеяния НЗ начинает играть примесное рассеяние.
Общий вид температурной зависимости подвижности НЗ приведен на рис.23.
ГАЛЬВАНОМАГНИТНЫЕ ЯВЛЕНИЯ
Эффект Холла
На носители заряда в магнитном поле действует сила Лоренца
![]()
где q - заряд носителя, ![]() -
его скорость, а
-
его скорость, а ![]() -
магнитная индукция в месте нахождения носителя. В отсутствие тока, в силу хаотичности
движения НЗ, какого-либо их перераспределения под действием силы Лоренца не
происходит, хотя траектории движения НЗ изменяются (искривляются). При
протекании тока средняя скорость НЗ отлична от нуля и равна
-
магнитная индукция в месте нахождения носителя. В отсутствие тока, в силу хаотичности
движения НЗ, какого-либо их перераспределения под действием силы Лоренца не
происходит, хотя траектории движения НЗ изменяются (искривляются). При
протекании тока средняя скорость НЗ отлична от нуля и равна
![]()
где ![]() - плотность
тока, п - концентрация НЗ. Поэтому в магнитном
поле возникнет холловская составляющая тока, перпендикулярная направлению
- плотность
тока, п - концентрация НЗ. Поэтому в магнитном
поле возникнет холловская составляющая тока, перпендикулярная направлению ![]() при
при
![]() =
0.
=
0.
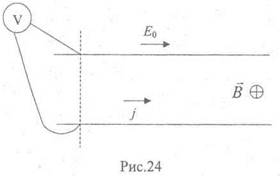
В рассматриваемой нами простой
геометрии эксперимента, когда напряженность приложенного электрического поля ![]() B (рис.24) и постоянный ток в направлении, перпендикулярном
B (рис.24) и постоянный ток в направлении, перпендикулярном ![]() , течь не
может, включение магнитного поля приведет к появлению на поверхности проводника
электрических зарядов. Холловский ток после переходного процесса исчезнет, но
возникнет холловская напряженность электрического поля
, течь не
может, включение магнитного поля приведет к появлению на поверхности проводника
электрических зарядов. Холловский ток после переходного процесса исчезнет, но
возникнет холловская напряженность электрического поля ![]() .
Значение ее таково, что сила, с которой это поле действует на НЗ q
.
Значение ее таково, что сила, с которой это поле действует на НЗ q![]() , полностью
компенсирует действие силы Лоренца. Следовательно,
, полностью
компенсирует действие силы Лоренца. Следовательно,
![]()
где
![]()
- постоянная Холла. Измеряя разность потенциалов между крайними точками поперечного сечения проводника Uн = EHd (смотри рис. 24), можно, зная j и В, найти концентрацию НЗ в полупроводнике.
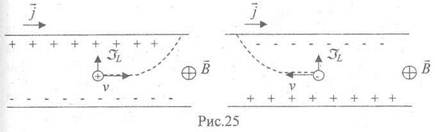
Более того, НЗ разного знака отклоняются магнитным полем при заданном направлении j в одну и ту же сторону, смотри рис.25. Поэтому полярность возникающего напряжения свидетельствует о знаке НЗ.
Приведенное выше простое рассмотрение эффекта Холла не требует привлечения кинетического уравнения Больцмана. Однако оно не дает ответа на вопрос: а изменилось ли сопротивление проводника в магнитном поле, или, другими словами, имеется ли продольное магнегосопротивление Δр, которое определяется как
![]()
где р0 - удельное сопротивление в отсутствие магнитного поля,
а ![]() (В) -
продольное удельное сопротивление, то есть коэффициент пропорциональности
между
(В) -
продольное удельное сопротивление, то есть коэффициент пропорциональности
между ![]() и
и
![]() (Е0=
(Е0=![]() (В)j), индекс означает параллельность
направлению тока.
(В)j), индекс означает параллельность
направлению тока.
Для ответа на этот вопрос необходимо использовать кинетическое уравнение Больцмана.
(подробности смотри в книге Морозова на странице)
В приведенной модели в книге Морозова магнетосопротивление отсутствует.
Для
перпендикулярной ![]() Холловской составляющей
Холловской составляющей ![]() получается: EH=RHBJ
получается: EH=RHBJ
RH – постоянная Холла.
В двухзонной модели магнетосопротивление ≠ 0. (вывод в книге Морозова)
Следовательно, в области больших магнитных полей величина магнетосопротивления выходит на постоянное значение.
Общий вид зависимости
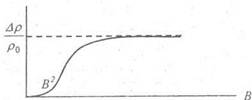
Рис. 27. Зависимость магнетосопротивления от индукции приложенного магнитного поля
ОПТИКА ПОЛУПРОВОДНИКОВ
Механизмы поглощения
Рассмотрим сначала возможность двухчастичного процесса, в котором квант света - фотон поглощается электроном. Такой процесс невозможен в случае свободных электронов (или любых других свободных заряженных частиц), так как он противоречит законам сохранения энергии и импульса. Действительно, пусть в процессе выполняется закон сохранения энергии, и энергия электрона возросла в результате поглощения на энергию фотона. При этом его импульс должен возрасти на величину ħω/v, где v - характерная скорость электрона. Но фотон обладая импульсом ħω/c, где с - скорость света. Поскольку v<<c (для энергии атомного масштаба скорость электрона v~10-2c), то закон сохранения импульса удовлетворить невозможно.
Основываясь на таком простом рассмотрении, можно сформулировать условие, при котором возможен двухчастичный процесс поглощения (и обратный ему процесс испускания): начальное заполненное и конечно пустое состояния электрона должны соответствовать практически одному и тому же значению волнового вектора (импульса), то есть принадлежать разным электронным зонам. Такие переходы называют прямыми или вертикальными.
![]()
Рассмотрим, что же будет происходить при
облучении бездефектного полупроводника с температурой Т<<Eg электромагнитной волной с частотой ω
(потоком фотонов). Если энергия кванта hω < Eg, то поглощение отсутствует. Значение является в случае полупроводника с
прямой щелью красной границей внутреннего фотоэффекта и называется краем
собственного поглощения. При ω = ωc электрон может перейти из состояния, лежащего вблизи
максимума валентной зоны, в состояние, расположенное вблизи минимума зоны
проводимости. Если же ω = ωc, то переходы происходят между состояниями, лежащими в этих двух зонах, отвечающими
практически одному и тому же значению волнового вектора ![]() и удовлетворяющими закону сохранения
энергии
и удовлетворяющими закону сохранения
энергии
![]()
где εc(![]() ) и εv(
) и εv(![]() ) - законы дисперсии электрона в зоне
проводимости и валентной зоне, соответственно. Эти переходы изображены на
рис.28а стрелкой. Зависимость коэффициента поглощения электромагнитной волны
от частоты изображена на рис.29а.
) - законы дисперсии электрона в зоне
проводимости и валентной зоне, соответственно. Эти переходы изображены на
рис.28а стрелкой. Зависимость коэффициента поглощения электромагнитной волны
от частоты изображена на рис.29а.
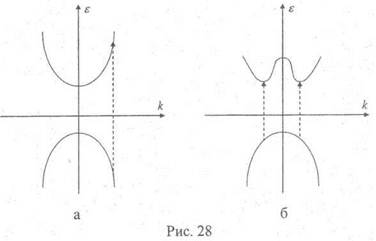
Если же щель непрямая, то двухчастичный процесс становится возможен при
![]()
Где минимум по ![]() берется по первой зоне Бриллюэна. Этот
процесс изображен на рис. 28б.
берется по первой зоне Бриллюэна. Этот
процесс изображен на рис. 28б.
Если двухчастичные процессы запрещены, то основной вклад в поглощение дают трехчастичные процессы, при которых поглощение электроном фотона сопровождается испусканием или поглощением третьей частицы, что позволяет удовлетворить обоим законам сохранения. Роль этой третьей частицы играетфонон - квант колебаний решетки. Вероятность таких процессов, называемых также непрямыми и невертикальными, намного ниже, чем двухчастных.
Именно такими трехчастичными процессами обусловлено поглощение при переходах электрона между состояниями одной зоны. Непрозрачность металлов обусловлена именно трехчастичными процессами. Поскольку в металлах заполненные и пустые состояния не разделены энергетической щелью, то поглощение начинается со сколь угодно низких частот. Вклад свободных носителей заряда в оптическое поглощение полупроводников мал из-за их низкой концентрации.
В полупроводниках с непрямой щелью трехчастичный процесс поглощения электроном фотона и фонона начинается с частоты
![]()
Где
ωph(![]() )
закон дисперсии фононов, a q - волновой
вектор, равный разности векторов,
соответствующих максимуму валентной зоны и минимуму зоны проводимости.
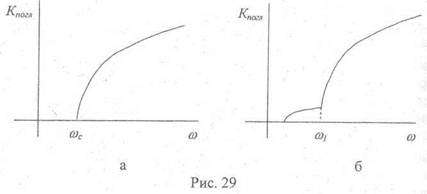
Зависимость коэффициента поглощения от частоты в случае полупроводника с непрямой
щелью изображена на рис.29б.
)
закон дисперсии фононов, a q - волновой
вектор, равный разности векторов,
соответствующих максимуму валентной зоны и минимуму зоны проводимости.
Зависимость коэффициента поглощения от частоты в случае полупроводника с непрямой
щелью изображена на рис.29б.
В германии и кремнии ωс лежит в инфракрасном диапазоне, поэтому они выглядят непрозрачными. В диэлектрике ωс лежит в ультрафиолетовом диапазоне, поэтому диэлектрик без примесей будет прозрачным и неокрашенным (как алмаз).
Окраска прозрачных драгоценных камней обусловлена примесями. Если в полупроводнике или диэлектрике имеются донорные или акцепторные примеси, то возможны переходы электронов из валентной зоны на акцепторный уровень или с донорного уровня в зону проводимости при поглощении ими фотонов с частотой ω < ωс. При этом закон сохранения импульса выполняется, так как при взаимодействии с дефектом недостающий импульс получается (передается) от кристалла в целом.
Коэффициент поглощения зависит от концентрации примесей, а окраска кристалла - от положения примесных уровней в запрещенной зоне. Так рубин и сапфир - это разновидности корунда (А12O3), содержащие примеси Cr3 + в первом случае и Fe3+ и Ti4+ - во втором.
Кроме того, примесь может играть роль той третьей частицы, взаимодействие с которой делает возможным непрямой переход.
Наряду с рассмотренными процессами существует механизм поглощения, обусловленный взаимодействием фотона с фононом (фононами), так называемое решеточное поглощение.
Что же происходит в дальнейшем с возникшей парой НЗ (электроном в зоне проводимости и дыркой в валентной зоне)? За счет взаимодействия с фононами они теряют свою избыточную энергию (если их кинетическая энергия при рождении превышает Т), и их распределение становится квазиравновесным, то есть распределение электронов в зоне проводимости (или распределения дырок в валентной зоне) описывается распределением Ферми-Дирака с неравновесным, вообще говоря, значением химического потенциала μ. Таким образом, за характерные времена электрон-фононного взаимодействия ~10-13 с электроны сосредотачиваются в пояске шириной порядка Т вблизи дна зоны проводимости, а дырки - в таком же пояске вблизи потолка валентной зоны.
За столь малое время количество электронов и дырок практически не изменяется. Это происходит за существенно большее время, называемое временем рекомбинации.
В чем же состоит процесс рекомбинации? Рекомбинация является процессом, обратным процессу генерации НЗ. При рекомбинации электрон и дырка исчезают, передавая свою энергию какой-либо частице. Этой частицей может быть фотон, такую рекомбинацию называют излучательной. Поскольку все электроны сосредоточены вблизи дна зоны проводимости, а дырки - вблизи потолка валентной зоны, то излучательная рекомбинация без участия каких-либо других частиц возможна только в прямозонных полупроводниках, где возможно удовлетворить в таком процессе законам сохранения. При этом излучение будет происходить на частоте, близкой к ωс.
Следовательно, если мы будем генерировать НЗ в прямозонном полупроводнике излучением на частоте ω >ωс, то он будет излучать на другой частоте ω’≈ωc . Это явление называется фотолюминесценцией.
Если же полупроводник непрямозонный, то излучательная рекомбинация невозможна без участия третьей частицы. Такой частицей может быть примесь (рекомбинация Холла - Шокли - Рида). Сначала примесь захватывает один из пары рекомбинирующих НЗ, а затем второй. В результате энергия электрон-дырочной пары уносится фотоном, а импульс передается кристаллу в целом.
Возможна безизлучательная рекомбинация, при которой энергия и импульс электрон-дырочной пары передаются другому НЗ (рекомбинация Оже).
В прямозонном полупроводнике InSb время излучательной рекомбинации при комнатной температуре составляет 6*10-7 с, а в непрямозонных полупроводниках кремнии и германии 3 часа и 0,43 с, соответственно. Введение в Ge примесей золота с концентрацией 10-7 уменьшает время излучательной рекомбинации до 10-8 - 10-9 с за счет процессов Холла-Шокли-Рида.
Диффузионный и дрейфовый токи. P-n переход.
До сих пор при рассмотрении явления электропроводности мы ограничивали себя случаем однородного вещества. Для создания тока в нем требовалось наличие внешней силы, действующей на НЗ. Ток, вызванный такой причиной, называется дрейфовым. Например, в случае наличия электрического поля плотность дрейфового тока в изотропном веществе равна
![]() др = σ
др = σ![]() = |q|γn
= |q|γn![]() ,
,
где q - заряд
носителя, п и γ - их концентрация и подвижность, соответственно,
![]() - напряженность электрического поля, а σ -электропроводность вещества. Эта формула нам хорошо
знакома, только плотность тока мы не называли дрейфовой.
- напряженность электрического поля, а σ -электропроводность вещества. Эта формула нам хорошо
знакома, только плотность тока мы не называли дрейфовой.
Дело в том, что в однородном веществе другой, диффузионной составляющей тока не было и плотность тока, равная сумме этих составляющих:
![]()
совпадала с ![]() др.
др.
В неоднородном веществе концентрация НЗ
в разных точках пространства может различаться. В этом случае диффузия НЗ,
вызванная их хаотическим движением, приводит к возникновению потока НЗ.
Плотность потока частиц
![]() равна, согласно закону Фика
равна, согласно закону Фика
![]()
где D - коэффициент диффузии частиц. Знак минус означает, что поток направлен навстречу градиенту концентрации, то есть из области, где концентрация частиц велика, в область, где она мала. Действительно, в результате хаотического теплового движения из области с высокой концентрацией к области низкой концентрации идет поток частиц. Встречный поток частиц из области низкой концентрации не так велик, так как плотность потока пропорциональна концентрации. В результате суммарный поток имеет указанное направление.
Так как НЗ обладают электрическим зарядом, их поток сопровождается переносом заряда, то есть возникает диффузионный электрический ток. Его плотность равна
![]()
Согласно соотношению, предложенному Эйнштейном, коэффициент диффузии классических частиц выражается через их подвижность
![]() (9.15)
(9.15)
Тот
факт, что D![]() Т очевиден, так как диффузия вызвана хаотическим
тепловым движением, мерой энергии которого и является температура. Учитывая соотношение (9.15) и выражая
Т очевиден, так как диффузия вызвана хаотическим
тепловым движением, мерой энергии которого и является температура. Учитывая соотношение (9.15) и выражая ![]() через потенциальную энергию НЗ w в электрическом поле
через потенциальную энергию НЗ w в электрическом поле
![]()
получаем для полной плотности тока:
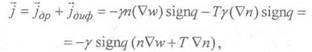
Где
![]()
В условиях равновесия концентрация носителей описывается распределением Больцмана:
![]() (9.18)
(9.18)
где
![]()
Поэтому в равновесии
![]() (9.19)
(9.19)
и после подстановки (9.19) в (9.16)
получаем ![]() =0. В то же время диффузионный и дрейфовый токи по
отдельности в неоднородной среде отличны от нуля и в равновесии.
=0. В то же время диффузионный и дрейфовый токи по
отдельности в неоднородной среде отличны от нуля и в равновесии.
Рассмотрим такую ситуацию на примере р-п перехода, то есть контакта между областями полупроводника, первая из которых легирована акцепторами, а вторая донорами.
Представим себе мысленно, что до момента времени t=0 эти области были разобщены, а затем приведены в соприкосновение (в реальной жизни такая процедура невозможна). Поскольку концентрация дырок в p-области, где они являются основными носителями, существенно выше, чем в n-области, где они являются неосновными носителями, то возникнет поток дырок из р- области в n-область. С электронами ситуация противоположна, и поток электронов потечет из n-области в p-область. На границе областей будет происходить рекомбинация НЗ.
Результирующий диффузионный ток, складывающийся из диффузных токов дырок и электронов, пойдет из p-области в п- область. В результате в изначально нейтральном полупроводнике начнется перераспределение зарядов: n-область будет заряжаться положительно, а p-область - отрицательно. Возникшая разность потенциалов вызовет дрейфовый ток, который будет направлен навстречу диффузионному. Перераспределение зарядов будет происходить до тех пор, пока диффузионный ток не будет точно скомпенсирован дрейфовым. На переходной процесс уйдут ничтожные доли секунды.
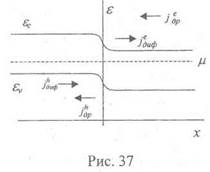
В установившемся равновесии (в отсутствие внешнего напряжения на р-п переходе) суммарный ток через р-п переход равен нулю, а диффузионный и дрейфовый токи противоположны и отличны от нуля. В результате на р-п переходе установилась контактная разность потенциалов, такая, что химический потенциал р в обеих областях одинаков. Возникшая картина электронных зон изображена на рис. 37.
Если теперь приложить к внешним границам полупроводника постоянное напряжение так, что «плюс» придется на р- область, а «минус» - на n-область, то возникшее электрическое поле будет направлено навстречу равновесному. В результате дрейфовый ток уменьшится и станет по модулю меньше диффузионного. Через р-п переход потечет ток, созданный в каждой из областей основными НЗ и достигающий значительной величины («пропускное» направление тока).
Если же теперь изменить полярность приложенного
напряжения («+» - к n-области, «-» - к р), то
созданное электрическое поле сложится с равновесным и «отгонит» основные носители от границы
между областями (дырки - в глубь p-области, электроны - в глубь n-области). В результате ток основных носителей прекратиться.
Весь перенос заряда будет происходить за счет неосновных носителей. Дрейфовый
ток в n-области будет обусловлен дырками, а в
p-области - электронами. Поэтому величина
тока будет намного меньше, чем в предшествующем случае («непропускное»
направление тока).